Sekarang kita telah siap untuk meneruskan ke bagian yang sangat penting yang merupakan lanjutan dari pembahasan kita tentang perkalian bilangan kompleks dalam bentuk polar.
Kita telah menetapkan bahwa:
karena pada perkalian, kita mengalikan modulus dan menambahkan argumen-argumennya.
karenDengan kata lain, jika ingin memangkat-tigakan bilangan kompleks dalam bentuk polar, kita cukup memangkat-tigakan modulusnya (nilai r) dan mengalikan argumennya (
) dengan 3.
Serupa halnya, untuk mengkuadratkan bilangan kompleks dalam bentuk polar, kita kuadratkan modulusnya (nilai r) dan mengalikan argumennya () dengan 2, yakni [r(cos + j sin )]² = r²(cos 2 + j sin 2).
Marilah kita perhatikan lagi hasil-hasil ini:
[r(cos + j sin )]² = r²(cos 2 + j sin 2)
[r(cos + j sin )]³ = r³(cos 3 + j sin 3)
serupa halnya:
Umumnya, kita dapat mengatakan:
) dengan 3.Serupa halnya, untuk mengkuadratkan bilangan kompleks dalam bentuk polar, kita kuadratkan modulusnya (nilai r) dan mengalikan argumennya (
) dengan 2, yakni [r(cos + j sin )]² = r²(cos 2 + j sin 2).Marilah kita perhatikan lagi hasil-hasil ini:
[r(cos
+ j sin )]² = r²(cos 2 + j sin 2)[r(cos
+ j sin )]³ = r³(cos 3 + j sin 3)serupa halnya:
Umumnya, kita dapat mengatakan:
Hasil umum ini sangat penting dan disebut teorema DeMoivre. Teorema ini mengatakan bahwa untuk memangkatkan suatu bilangan kompleks dalam bentuk polar ke pangkat n, kita pangkatkan r dengan pangkat n dan mengalikan sudutnya dengan n.
Contoh 1:
Karena inilah bentuk polar menjadi terkenal! Teorema DeMoivre juga berlaku ketika kita memangkatkan bilangan kompleks ke pangkat pecahan, yakni ketika kita sedang mencari akar suatu bilangan kompoleks.
Misalnya, untuk mencari akar kuadrat z = 4 (cos 70°+ j sin 70°)
Teorema ini berlaku kapan saja, tidak menjadi masalah apakah pangkatnya positif, negtif, bilangan bulat atau pecahan. Sebenarnya Teorema DeMoivre sangatlah penting. Marilah kita tulis teorema itu sekali lagi. Begini, untuk sebarang nilai n berlaku:
Lihat kembali pencarian akar suatu bilangan kompleks. Marilah kita cari akar pangkat tiga dari z = 8(cos 120° + j sin 120°). Inilah bilangan kompleks yang diketahui yang diperlihatkan pada diagram Argand:
Tentu saja, kita dapat mengatakan bahwa adalah '1 putaran + 120°': vektornya akan tetap pada kedudukan yang sama, atau, untuk hal itu(2 putaran + 120°), (3 putaran + 120°), dan seterusnya.
Misalnya z = 8|120° atau 8|480° atau 8|840° atau 8|1200° dan sterusnya. Dan jika kita sekarang menggunakan Teorema DeMoivre untuk masing-masing bilangan kompleks ini, kita peroleh:
Jika hasil di atas disederhanakan, kita peroleh:
Jika masing-masing bilangan kompleks di atas kita buat pada diagram Argand, sebagai berikut:
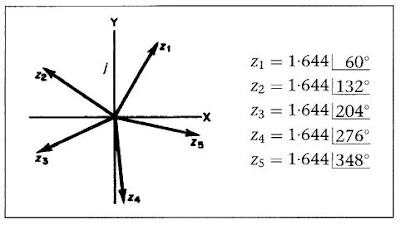
Kita lihat, kita memiliki tiga hasil yang sangat berbeda untuk akar pangkat-tiga dari z dan juga bahwa diagram keempat akan merupakan pengulangan dari diagram pertama. Sebarang perhitungan berikutnya hanyalah mengulangi ketiga posisi ini.
Sketsa ketiga vektor pertama dari akar pangkat-tiga z = 8(cos 120° + j sin 120°) di atas pada diagram Argand tunggal, dapat digambarkan sebagai berikut:
Oleh sebab itu, kita lihat bahwa terdapat 3 akar pangkat-tiga dari suatu bilangan kompleks. Juga, jika Anda memperhatikan sudutnya, Anda akan lihat bahwa ketiga akar itu sama jaraknya pada diagram tersebut, sebarang dua vektor yang bersebelahan dipisahkan sebesar 120°.
Benar. Oleh sebab itu yang perlu kita lakukan pada prakteknya ialah mencari akar yang pertama dan cukup menambahkan 120° untuk memperoleh akar berikutnya -dan seterusnya.
Misalnya, untuk mencari akar kuadrat z = 4 (cos 70°+ j sin 70°)
Teorema ini berlaku kapan saja, tidak menjadi masalah apakah pangkatnya positif, negtif, bilangan bulat atau pecahan. Sebenarnya Teorema DeMoivre sangatlah penting. Marilah kita tulis teorema itu sekali lagi. Begini, untuk sebarang nilai n berlaku:
Tentu saja, kita dapat mengatakan bahwa
adalah '1 putaran + 120°': vektornya akan tetap pada kedudukan yang sama, atau, untuk hal itu(2 putaran + 120°), (3 putaran + 120°), dan seterusnya. Misalnya z = 8|120° atau 8|480° atau 8|840° atau 8|1200° dan sterusnya. Dan jika kita sekarang menggunakan Teorema DeMoivre untuk masing-masing bilangan kompleks ini, kita peroleh:
Jika masing-masing bilangan kompleks di atas kita buat pada diagram Argand, sebagai berikut:
Sketsa ketiga vektor pertama dari akar pangkat-tiga z = 8(cos 120° + j sin 120°) di atas pada diagram Argand tunggal, dapat digambarkan sebagai berikut:
Benar. Oleh sebab itu yang perlu kita lakukan pada prakteknya ialah mencari akar yang pertama dan cukup menambahkan 120° untuk memperoleh akar berikutnya -dan seterusnya.
Perhatikan bahwa ketiga akar pangkat-tiga suatu bilangan kompleks mempunyai modulus (ukuran) yang sama dan terpisah dengan jarak yang sama pada interval  yakni 120°.Contoh 2: Untuk mencari ketiga akar pangkat-tiga dari suatu bilanangan kompleks z = 5(cos 225° + j sin 225°), akar pertama diberikan oleh    Kita kethui bahwa akar pangkat-tiga lainnya mempunyai panjang (modulus) yang sama, yakni 1,71, dan dipisakan dengan interval yakni 120°.Jadi ketiga akar pangkat-tiga tersebut ialah:   Inilah diagramnya  Kita cari akar sebarang dari suatu bilangan kompleks dengan cara yang sama: (a) Gunakan Teorema DeMoivre untuk mencari akar pertama dari n akarnya.
(b) Akar lain dengan demikian akan terdistribusi di sekeliling diagran dengan interval yang tetap sebesar
 .
Oleh sebab itu, suatu bilangan kompleks memiliki:
|
, 
, 
, 
, 
No comments:
Post a Comment
Yuk kita saling berkomentar dengan baik dan sopan untuk menumbuhkan ukhuwah dan silaturahmi sesama sahabat blogger. Terima Kasih.