Integrasi hasilkali - Integrasi per bagian
Seringkali kita perlu mengintegrasi suatu hasilkali yang salah satu faktornya bukan merupakan turunan dari faktor yang satu lagi. Sebagai contoh, dalam kasus
ln x bukan turunan dari x2
x2 bukan turunan dari ln x
jadi dalam situasi seperti ini, kita harus mencari metode lain untuk dapat menyelesaikan integral ini. Marilah kita membuat aturan untuk kasus-kasus yang demikian.
Jika u dan v adalah fungsi dari x, maka kita tahu bahwa:
Sekarang integrasikan kedua ruas terhadap x. Di ruas kiri kita akan memperoleh kembali fungsi asalnya:
dan dengan mengatur kembali suku-sukunya, kita akan memperoleh:
Di ruas kiri, terdapat hasilkali dari dua faktor yang akan kita integrasikan. Salah satu faktor dipilih sebagai fungsi u, faktor yang satu lagi sebagai turunan dari fungsi v. Tentunya untuk mencari v, kita harus mengintegrasi faktor ini secara terpisah. Kemudian, dengan mengetahui u dan v kita dapat mensubstitusikan keduanya ke dalam ruas kanan dan dengan demikian selesailah prosesnya.
Anda akan menjumpai suatu hasilkali lain yang masih harus diintegrasikan lagi, tetapi, kecuali kalau kita tidak beruntung, hasilkali ini akan lebih mudah untuk diselesaikan daripada yang permulaan.
Inilah kunci dari prosesnya:
Untuk mudahnya, rumus ini dapat diingat sebagai:
Penulisan seperti ini lebih mudah diingat, tetapi bentuk yang sebelumnya mempunyai arti yang lebih rinci. Metode ini disebut integrasi per bagian (integration by parts).
Salinlah hasil-hasil ini ke dalam buku catatan Anda. Anda akan segera mempelajarinya. Sekarang kita lanjutkan dengan beberapa contoh tentang integrasi per bagian.
Contoh 1
Kedua faktornya adalah x2 dan ln x, dan kita harus menentukan yang mana sebagai u dan yang mana sebagai dv. Jika kita pilih x2 sebagai u dan ln x dx sebagai dv, maka kita perlu mengintegrasikan ln x untuk memperoleh v. Tetapi syangnya,  tidak terdapat dalam daftar integral-integral standar, sehingga kita harus menentukan u dan dv dengan cara lain, yaitu u = ln x sehingga
tidak terdapat dalam daftar integral-integral standar, sehingga kita harus menentukan u dan dv dengan cara lain, yaitu u = ln x sehingga  dan
dan  sehingga
sehingga  Konstanta integrasi tidak perlu dituliskan di sini, karena kita berada di tengah-tengah perhitungan integral. Pada akhirnya konstanta integrasi akan muncul dengan sendirinya.
Konstanta integrasi tidak perlu dituliskan di sini, karena kita berada di tengah-tengah perhitungan integral. Pada akhirnya konstanta integrasi akan muncul dengan sendirinya.
 tidak terdapat dalam daftar integral-integral standar, sehingga kita harus menentukan u dan dv dengan cara lain, yaitu u = ln x sehingga
tidak terdapat dalam daftar integral-integral standar, sehingga kita harus menentukan u dan dv dengan cara lain, yaitu u = ln x sehingga  dan
dan  sehingga
sehingga  Konstanta integrasi tidak perlu dituliskan di sini, karena kita berada di tengah-tengah perhitungan integral. Pada akhirnya konstanta integrasi akan muncul dengan sendirinya.
Konstanta integrasi tidak perlu dituliskan di sini, karena kita berada di tengah-tengah perhitungan integral. Pada akhirnya konstanta integrasi akan muncul dengan sendirinya.
Perhatikan bahwa jika salah satu faktor dari hasilkali yang akan diintegrasikan adalah suatu logaritma, maka faktor ini harus dipilih sebagai u.
Contoh 2
Lanjutkan ke Frame 24
Dalam contoh 1 kita telah melihat bahwa jika salah satu faktornya adalah suatu fungsi logaritma, maka fungsi logaritma itu harus dianggap sabagai u.
Dalam contoh 2 kita telah melihat bahwa, asalkan tidak terdapat suku logaritma, pangkat dari x dianggap sebagai u (sebenarnya, metode ini berlaku dengan baik hanya untuk pangkat-pangkat dari x yang merupakan bilangan bulat positif saja. Untuk pangkat-pangkat yang lainnya harus menggunakan metode yang lain).
Jadi yang manakah diantara dua faktor yang harus dipilih sebagai dalam masing-masing kasus berikut?
Baiklah. Sekarang untuk contoh yang ketiga.
Contoh 3
 Di sini tidak terdapat faktor logaritma maupun pangkat dari x. Marilah kita coba dengan menetapkan
Di sini tidak terdapat faktor logaritma maupun pangkat dari x. Marilah kita coba dengan menetapkan  dan
dan  sehingga
sehingga 
(dan sekali lagi dengan integrasi per bagian)
dan kelihatannya kita kembali lagi ke bentuk semula.
Maka, dengan mnyederhanakan persamaan ini, kita peroleh:
Setiap kali kita mengintegrasi fungsi-fungsi berbentuk  atau
atau  kita akan memperoleh hasil-hasil perhitungan dengan tipe yang mirip sesudah menerapkan aturannya dua kali.
kita akan memperoleh hasil-hasil perhitungan dengan tipe yang mirip sesudah menerapkan aturannya dua kali.
 atau
atau  kita akan memperoleh hasil-hasil perhitungan dengan tipe yang mirip sesudah menerapkan aturannya dua kali.
kita akan memperoleh hasil-hasil perhitungan dengan tipe yang mirip sesudah menerapkan aturannya dua kali.
Lanjutkan ke Frame 26
Ketiga contoh yang kita bahas di atas memungkinkan kita untuk membuat urutan prioritas untuk u:
maka:
- Jika salah satu faktor adalah suatu fungsi logaritma, faktor itu harus diambil sebagai 'u'.
- Jika tidak terdapat fungsi logaritma tetapi ada pangkat dari x, pangkat dari x itu harus dijadikan 'u'.
- Jika tidak terdepat fungsi logaritma maupun pangkat dari x, maka fungsi eksponensial dajadikan sebagai 'u'.
Dengan mengingat urutan prioritas kita akan terhindar dari banyak kesalahan awal.
Jadi faktor mana yang akan Anda pilih sebagai 'u' dalam soal-soal berikut?
Baiklah, sekarang lihat pada integral yang ini:
Dengan mengikuti aturan mengenai urutan prioritas untuk u, maka dalam kasus ini kita harus nemilih u = .....
Benar. Buatlah catatan mengenai daftar prioritas untuk u tersebut dalam buku catatan Anda. Kemudian lanjutkan dan tentukan penyelesaian dari integral di atas.
Jika Anda sudah selesai, periksalah pekerjaan Anda dengan yang terdapat pada frame berikut
Berikut ini adalah penyelesaiannya. Perhatikanlah dengan seksama.
Sekarang cobalah integral berikut dengan cara yang serupa. Selesaikanlah kedua-duanya terlebih dahulu sebelum melanjutkan ke frame berikutnya.
Penyelesaiannya terdapat di frame 30
Itulah hasilnya. Sekarang Anda dapat mengerjakan integral hasilkali


















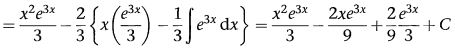

























No comments:
Post a Comment
Yuk kita saling berkomentar dengan baik dan sopan untuk menumbuhkan ukhuwah dan silaturahmi sesama sahabat blogger. Terima Kasih.