Integrasi dengan pecahan parsial
Misalkan kita harus mengintegrasi  Jelas integral ini bukanlah salah satu dari tipe standar yang sudah kita pelajari, dan pembilangnya bukanlah turunan dari penyebutnya. Jadi bagaimana kita dapat menyelesaikannya?
Jelas integral ini bukanlah salah satu dari tipe standar yang sudah kita pelajari, dan pembilangnya bukanlah turunan dari penyebutnya. Jadi bagaimana kita dapat menyelesaikannya?
 Jelas integral ini bukanlah salah satu dari tipe standar yang sudah kita pelajari, dan pembilangnya bukanlah turunan dari penyebutnya. Jadi bagaimana kita dapat menyelesaikannya?
Jelas integral ini bukanlah salah satu dari tipe standar yang sudah kita pelajari, dan pembilangnya bukanlah turunan dari penyebutnya. Jadi bagaimana kita dapat menyelesaikannya?
Dalam kasus ini, pertama kali kita tulis pecahan aljabar yang agak rumit ini ke dalam bentuk pecahan-pecahan parsialnya, yaitu sejumlah pecahan aljabar yang lebih sederhana yang akan dapat diintegralkan secara terpisah tanpa kesulitan. Sebenarnya,  dapat ditulis sebagai
dapat ditulis sebagai 
 dapat ditulis sebagai
dapat ditulis sebagai 
Metode ini tentu saja, bergantung kepada kemampuan kita untuk menuliskan fungsi yang bersangkutan ke dalam bentuk pecahan parsial.
Aturan-aturan dari pecahan parsial adalah sebagai berikut:
- Pembilang dari fungsi yang diberikan harus memiliki derajat yang lebih rendah daripada penyebutnya. Jika tidak demikian, maka pertama-tama bagilah dengan menggunakan pembagian panjang.
- (a) Faktorkan penyebutnya menjadi faktor-faktor prima. Ini penting, karena faktor-faktor yang diperoleh akan menentukan bentuk dari pecahan parsial.
- (b) Faktor linear
menjadi pecahan parsial berbentuk
- (c) Faktor
menjadi pecahan parsial
- (d) Faktor
menjadi pecahan parsial
- (e) Faktor kuadratik
menjadi pecahan parsial
Salinlah aturan-aturan ini ke dalam buku catatan Anda untuk referensi. Hal itu akan sangat bermanfaat.
Lanjutkan ke frame berikutnya
Sekarang untuk beberapa contoh
Contoh 1
Kalikan kedua ruas dengan penyebut (x - 1)(x - 2):
Persamaan ini merupakan identitas dan benar untuk semua nilai x yang ingin kita substitusikan. Jika mungkin, pilihlah satu nilai x yang akan membuat salah satu dari tanda-tanda kurungnya menjadi nol.
Misalkan (x - 1) = 0; artinya substitusikan x = 1.
Misalkan (x - 2) = 0; artinya substitusikan x = 2.
Jadi integralnya sekarang dapat ditulis .......
Sekarang sisanya akan mudah
(jangan lupa konstanta integrasinya!)
Contoh 2
Untuk menentukan
Pembilang = derajat kedua; penyebut = derajat ketiga. Aturan (a) dipenuhi.
Penyebut sudah difaktorkan menjadi faktor-faktor primanya. Aturan (b) dipenuhi.
Setelah substitusi-substitusi ini selesai, kita dapat mencari konstanta-konstanta sisanya (dalam kasus ini, hanya B) dengan cara menyamakan koefisien-koefisien. Pilihlah pangkat yang paling tinggi, yaitu x2 dalam contoh ini.
Contoh 3
Aturan-aturan (a) dan (b) dari pecahan parsial terpenuhi. Tahap berikutnya adalah menuliskannya dalam bentuk pecahan parsial.
Sekarang hilangkan penyebut-penyebutnya dengan mengalikan kedua ruas dengan (x + 2)3. Jadi diperoleh:
x2 + 1 = .......
Sekarang kita tetapkan (x + 2) = 0, maka x = -2
Dalam identitas ini tidak terdapat kurung yang lain, jadi sekarang kita samakan koefisien-koefisiennya, dimulai dengan pangkat tertinggi, yaitu x2. Apakah yang kita dapatkan?
Karena
Sekarang kita samakan koefisien pangkat yang paling rendah, dalam hal ini adalah suku konstanta (atau suku-suku absolut) pada kedua ruas:
Sekarang untuk satu contoh lagi, lanjutkan ke Frame 40
Contoh 4
Dalam contoh ini terdapat faktor kuadratis yang tidak dapat difaktorkan lagi
Misalkan (x - 2) = 0, atau lebih tepatnya x = 2
Samakan koefisien-koefisiennya
CT = Constant Terms (suku konstanta)
Berikut ini satu soal lagi untuk Anda kerjakan sendiri.
Contoh 5
Aturan-aturan (a) dan (b) dipenuhi, dan bentuk pecahan parsialnya adalah
Sekarang lanjutkan sendiri. Jika Anda telah menyrlesaikannya, lanjutkan ke Frame 42
Periksalah pekerjaan Anda dengan teliti
Misalkan (2x - 1) = 0, dengan kata lain, x = 1/2
Lanjutkan ke Frame 43
Kita telah mempelajari beberapa integral dari satu atau beberapa tipe dalam studi kita sampai saat ini. Kita telah mempelajari:
- Integral standar yang dasar
- Funsi dari suatu fungsi linear dalam x
- Integral yang salah satu bagiannya adalah turunan dari bagian yang lain
- Integrasi per bagian, yaitu integrasi hasilkali
- Integrasi dengan pecahan parsial
Sekarang, lanjutkan ke Frame 44





















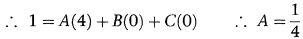



























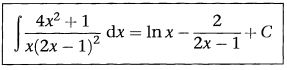



terimaksih, sangat membantu
ReplyDeleteThankss gan
ReplyDeleteTerimaksih banyakkk sangat membantu 😊
ReplyDeleteTerima kasih banyak, sangat membantu
ReplyDeleteok kembali kasih
Delete